ToyDB : Skip List Index

기존 프로젝트에 포함되었던 B+Tree 구조를 완성한 후, 새로운 인덱스 구조인 Skip List를 완성했다. 아예 새로운 구조로 구현한 것이라 꽤 오래 걸렸다. 물론, 귀찮아서 블로그 포스팅을 늦게 한 탓도 있지만… 소스코드는 여기에 업데이트하고 있다. 프로젝트에 대한 조언은 언제나 환영한다.

Skip List Logic

이전 B+Tree Index 글과 마찬가지로 Skip List에 대한 정리나, 강의자료가 아니기 때문에, Skip List의 로직을 자세히 설명하지는 않을 것이다. 찾아보고 싶다면, 여기에서 간략한 설명을 보거나, 직접 구글링을 해서 찾는 편이 더 좋을 것이다. 그렇지만, 기본적인 로직 정도는 설명하는 게 필요할 듯 해서 간단히 언급하고 넘어가겠다.

이름에서부터 티가 나지만, 기본적으로 Skip List는 Linked List이다. 다만, Linked List의 단점인 탐색 시간복잡도 O(N)을 개선한 구조이다. 여기에서 무작위성이 사용되는데, 텍스트만으로 설명하기는 어려우니 그림을 조금 이용하겠다. 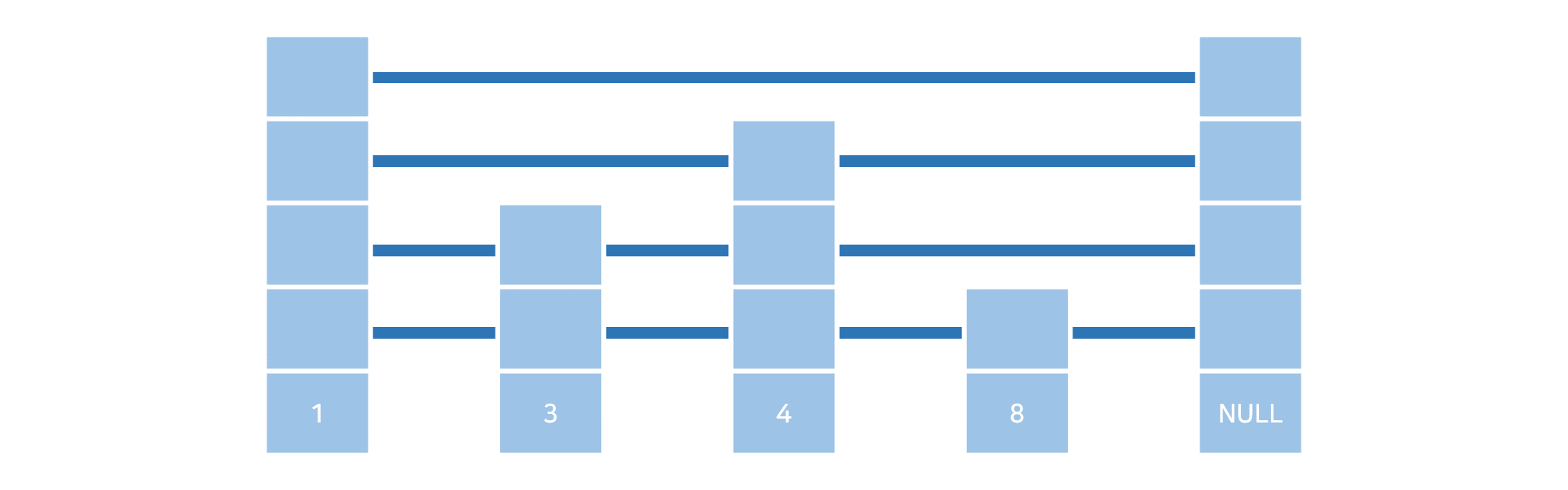Skip List는 Linked List와 달리 여러 개의 노드와 연결되어 있다. 여기서 각 노드는 “레벨”이라는 것이 있고, 각 레벨마다 Linked List처럼 연결이 되어 있는 것이다. 또한 각 레벨은, 노드가 생성될 때 무작위로 부여된다. 이러한 구조가 어떻게 시간복잡도 개선이 가능한가? 에 대해선 바로 아래의 그림을 보면 알 수 있다. 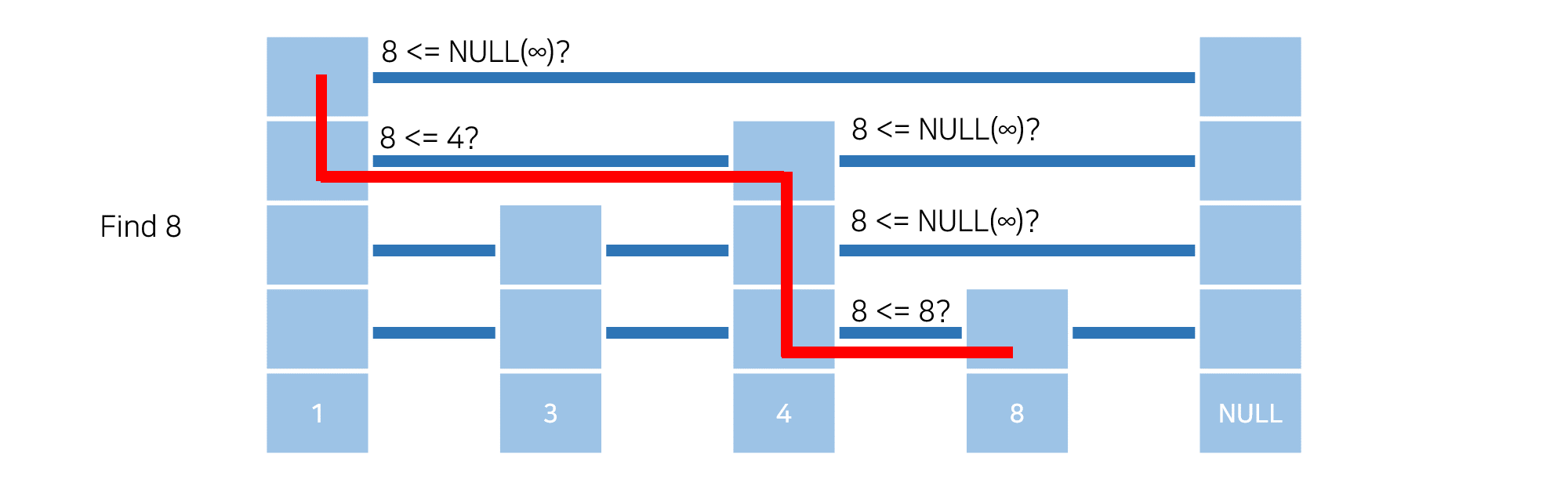가장 높은 레벨에서부터 다음 노드를 보면서 다음 노드의 값이 찾는 값보다 크다면 바로 아래 레벨로 내려가고, 찾는 값 이하라면 다음 노드로 넘어가는 과정을 반복하는 식으로 찾게 되는 것이다. 이렇게 하면 탐색을 위해 거치는 노드의 개수를 줄일 수 있게 되고, 시간복잡도의 기댓값이 O(log N) 정도로 줄어들게 된다. 실제로 위의 예시에서도 원래는 4개의 노드를 거쳐야 찾을 수 있는 8을 3개의 노드만을 거쳐서 찾을 수 있게 된다. 물론 드라마틱한 차이는 아니지만, 노드의 수가 많아지고, 최대 레벨값이 커진다면 그 효과는 더욱 커질 것이다. 데이터의 삽입이나 삭제 또한 위와 같은 논리로 진행하기 때문에 데이터가 정렬된 상태로 유지된다는 것이 보장된다.

Skip List Implementation

로직은 확실하게 알고 있으니 이제 그대로 구현만 하면 된다… 라고 생각했다면 오산이다. Skip List 자료구조를 구현하는 게 아닌, Skip List Index를 구현하는 것이기 때문이다. 우선 모든 노드는 “페이지”라는 규격에 맞아야 했고, 이 규격은 4096Byte라는 매우 큰 크기를 갖고 있었다. 따라서, Skip List의 노드를 이 페이지에 맞도록 재조정할 필요가 있었다.

위의 예시에서도 알 수 있듯이, 본래 Skip List는 한 노드에 하나의 값을 가지고 있다. 그래야 삽입/삭제 연산이 쉽기 때문이다. 그런데 DBMS의 인덱스로 쓰이기 위해서는 한 노드에 하나의 레코드만 들어 있어서는 안된다. 만약 한 DB에 레코드가 1억개 들어있다고 가정하게 되면 DB의 크기가 1억*4KB = 400TB라는 무시무시한 크기를 갖게 되기 때문이다. 이렇게 되면 너무 메모리 효율이 좋지 않다. 따라서 한 페이지에 여러개의 레코드를 포함할 수 있도록 설계를 했다. 최대 27개의 레코드(하나 당 128Byte)가 한 페이지에 포함되도록 디자인했고, 탐색은 각 페이지가 포함하는 Key 중 가장 작은 값을 기준으로 탐색하도록 했다. 즉 기존의 B+Tree Index와 로직을 비슷하게 한 것이다.

또한, 노드의 최대 레벨은 16으로 했다. 너무 크게 잡을 경우 오히려 한 페이지가 포함할 수 있는 레코드의 개수가 적어지게 되므로 어느정도의 균형을 맞추기 위해 이렇게 설계했다. 후에 기회가 된다면 레벨의 크기에 따른 성능 차이를 보는 것도 좋을 것이다.

Next Step

1. Iterator
   본래는 인덱스 구조를 하나 더 설계해서 구현할 생각이었다. 하지만 너무 인덱스 설계에만 몰입하는 느낌이 있어서 잠깐 다른 부분을 구현해보려고 한다. Join이나 Scan 등의 연산자에 필수적이라고 할 수 있는 Iterator를 구현할 생각이다. 논문에서 보았던 Iterative Model을 구현하는데 도움이 될 것이라고 생각한다.
2. Next Next(?) Index : Radix Tree
   논문에서도 상당히 많이 언급된 Radix Tree, 흔히 Trie라고 부르는 구조를 Index로 구현해볼 생각이다. 이것도 여기에 구현은 해봤으니 큰 어려움은 없겠지만… 역시 노드 구조나 API 변형이 조금 걱정이다.